Public-key Cryptosystems
Abstract
In computer communications, cryptography is indispensable for
deterring wiretappers and for detecting unauthorized modifications.
Public-key cryptosystems in particular, make it easy to manage keys
securely, and are widely in use.
In order to invent faster and more secure public-key cryptosystems, we
have conducted research on public-key cryptosystems based on elliptic
curves.
Our main results are as follows.
Equivalence of Counting the Number of Points on Elliptic Curve
over the Ring Zn and Factoring n
Elliptic curves and cubic curves can be applied to public-key
cryptosystems, and as such several schemes have been
proposed [1].
There are two typical elliptic curve cryptosystems: ElGamal-type
schemes and RSA-type schemes.
The security of the former schemes is based on the difficulty of
solving an elliptic curve discrete logarithm problem modulo a large
prime.
However, the security of the latter schemes is based on the difficulty
of factoring a large composite.
RSA-type elliptic curve schemes can be broken if the
eavesdropper knows the order of elliptic curves used, instead
of knowing the prime factors of used composites.
No relation had been known between these two difficulties, 1) the difficulty of
the obtaining the order of elliptic curve modulo n, and 2) the
difficulty of factoring the composite.
Recently, we proved that the two difficulties are computationally
equivalent [2].
Accordingly, we proved that factoring a large composite leads to the
obtainment of the elliptic curve order modulo n.
Conversely, we proved that obtaining the elliptic curve order modulo
n leads to success in factoring a large composite n.
This result implies that we must carefully design the RSA-type
elliptic curve scheme so that the eavesdropper cannot obtain the elliptic
curve order modulo n.
Furthermore, we showed the relation between factoring a composite
and solving the elliptic curve logarithm problem modulo the
composite.
As a result, 1) you can factor the composite n if you solve the
discrete logarithm problem modulo n, and 2) you can solve the
discrete logarithm problem modulo a composite n if you can factor the composite and solve the discrete logarithm problem
modulo a prime.
Hence, this results in greater safety standards for public-key
cryptosystems.
Security analysis based on diophantine equation for RSA-type cryptosystems
A broadcast message attack against RSA-type cryptosystems was proposed in 1997
[3].
In this attack, an adversary obtains a diophantine equation from broadcasted ciphertexts
and then computes the plaintext by solving the equation.
However, this attack can be made ineffective by properly choosing the plaintext space.
We show another attack based on computing integral points of elliptic curves
[4].
This new attack can be effectively applied when both coefficients and the rank of the elliptic curve are small.
We show that all plaintext that is a torsion point of elliptic curves is weak against the new attack.
We will conduct numerical experiments and a complexity analysis of the new attack algorithm.
[1]
Koyama, K.: Fast RSA-type schemes based on singular cubic curves 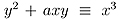 (mod n),
Advances in Cryptology --- EUROCRYPT'95, LNCS 921, pp.329-340 (1995).
(mod n),
Advances in Cryptology --- EUROCRYPT'95, LNCS 921, pp.329-340 (1995).
[2]
Kunihiro, N. and Koyama, K.: Equivalence of Counting
the Number of Points on Elliptic Curve over the Ring Zn and
Factoring n, Advances in Cryptology --- EUROCRYPT'98, LNCS 1403,
pp. 47-58 (1998).
[3]
Bleichenbacher, D.: On the Security of the KMOV Public Key Cryptosystem, Advances in Cryptology --- CRYPTO'97, LNCS 1294, pp. 235-248 (1997).
[4]
Tsuruoka, Y. and Koyama, K.:
Security analysis based on diophantine equation for RSA-type elliptic curve cryptosystems (in Japanese),
the 1998 Symposium on Cryptography and Information Security, SCIS'98-4.1.E (1998).
Copyright(C) 1998 Nippon Telegraph and Telephone Corporation
Last modified on
31/Mar/2000
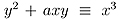 (mod n),
Advances in Cryptology --- EUROCRYPT'95, LNCS 921, pp.329-340 (1995).
(mod n),
Advances in Cryptology --- EUROCRYPT'95, LNCS 921, pp.329-340 (1995).