Abstract
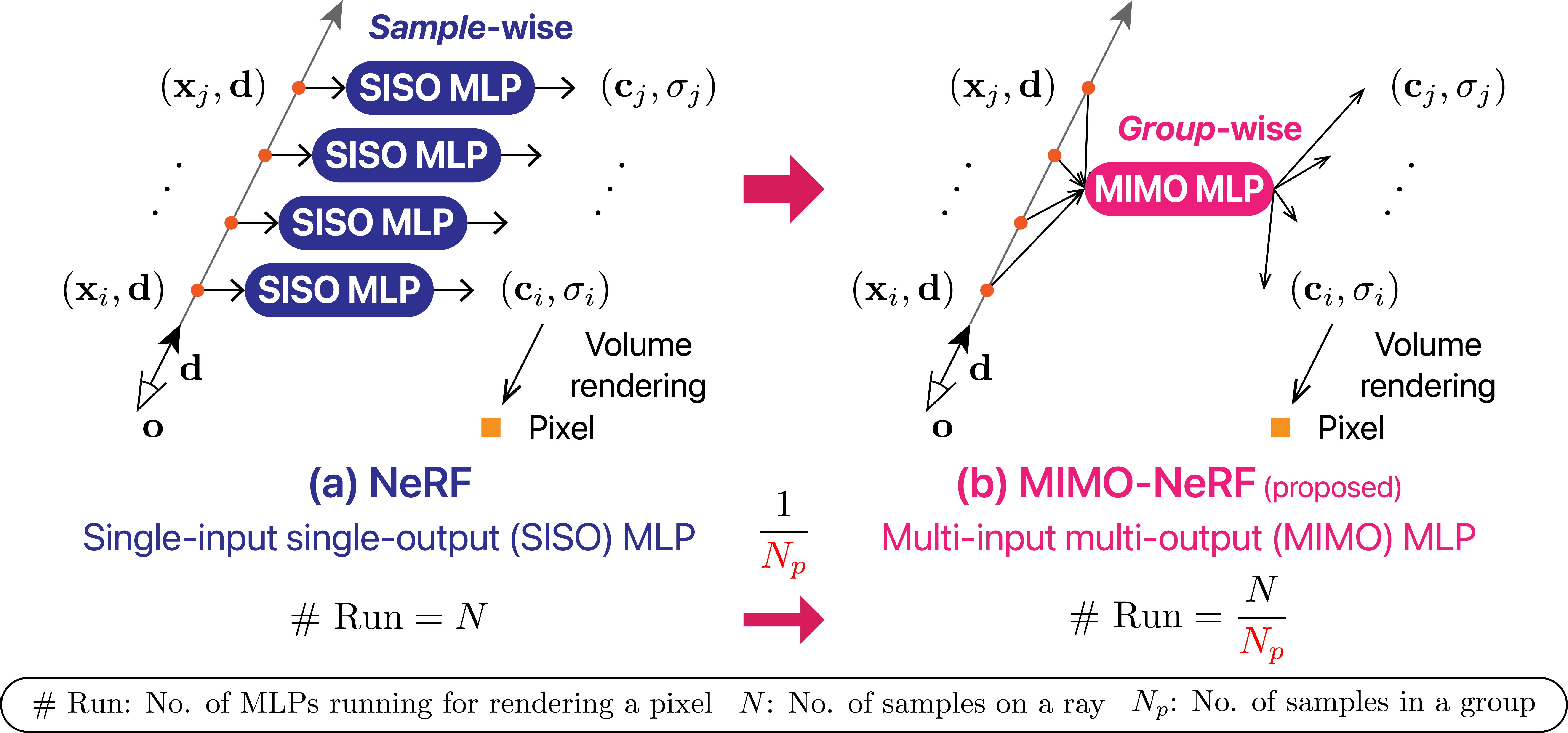
Neural radiance fields (NeRFs) have shown impressive results for novel view synthesis. However, they depend on the repetitive use of a single-input single-output multilayer perceptron (SISO MLP) that maps 3D coordinates and view direction to the color and volume density in a sample-wise manner, which slows the rendering. We propose a multi-input multi-output NeRF (MIMO-NeRF) that reduces the number of MLPs running by replacing the SISO MLP with a MIMO MLP and conducting mappings in a group-wise manner. One notable challenge with this approach is that the color and volume density of each point can differ according to a choice of input coordinates in a group, which can lead to some notable ambiguity. We also propose a self-supervised learning method that regularizes the MIMO MLP with multiple fast reformulated MLPs to alleviate this ambiguity without using pretrained models. The results of a comprehensive experimental evaluation including comparative and ablation studies are presented to show that MIMO-NeRF obtains a good trade-off between speed and quality with a reasonable training time. We then demonstrate that MIMO-NeRF is compatible with and complementary to previous advancements in NeRFs by applying it to two representative fast NeRFs, i.e., a NeRF with sample reduction (DONeRF) and a NeRF with alternative representations (TensoRF).
Challenge of training MIMO-NeRF
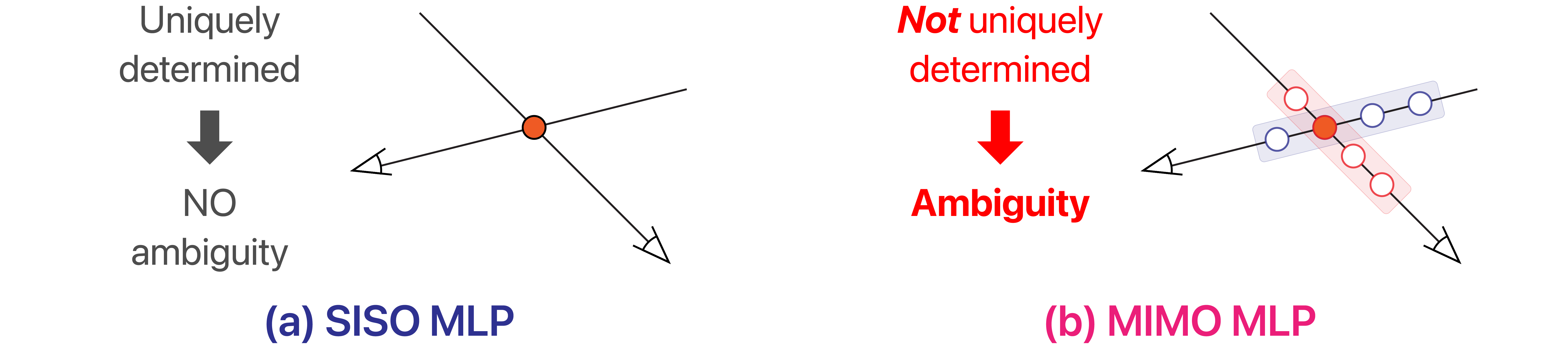
When a SISO MLP is used, the color and volume density of each point are uniquely determined because the values are explained by unique input coordinates (Figure 2(a)). In contrast, when a MIMO MLP is used, they are not uniquely determined because they can differ according to the choice of input coordinates that vary by viewpoint, grouping, and sampling (Figure 2(b)). This leads to some ambiguity and causes fluctuation artifacts (Figure 4(a)).
Solution: Self-supervised learning
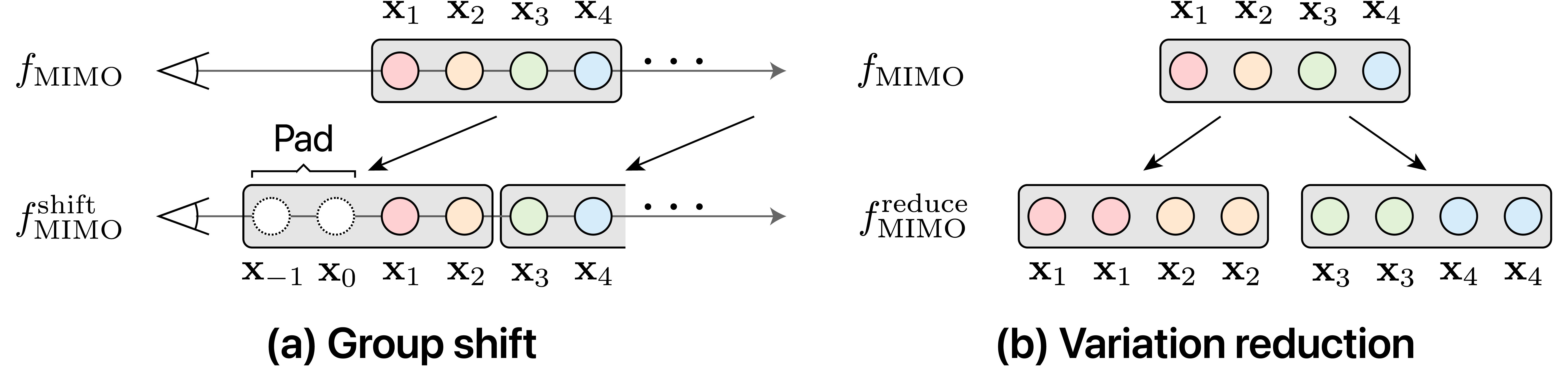
One possible solution is to train a standard (i.e., SISO) NeRF first and then distill the model onto the corresponding MIMO-NeRF. However, this increases training time because both student and teacher NeRFs must be trained. Alternatively, we have developed a novel self-supervised learning approach in which we reformulate a MIMO MLP in several ways (in particular, we use group shift (Figure 3(a)) and variation reduction (Figure 3(b)) and impose a consistent regularization so that the reformulated MIMO MLPs produce the same outputs. Because each reformulated MIMO MLP can render a pixel faster than the original SISO MLP, we can prevent a large sacrifice of training time even when using multiple reformulated MIMO MLPs by adequately adjusting the reformulation configuration.
Impact of self-supervised learning
Figure 4 shows an example of the effects of the proposed self-supervised learning (SSL). MIMO-NeRF-naive (i.e., MIMO-NeRF without SSL) suffers from ambiguity in the color and volume density of each point and deteriorates image quality (Figure 4(a)). In contrast, MIMO-NeRF-self (i.e., MIMO-NeRF with SSL) alleviates fluctuation artifacts and improves image quality (Figure 4(b)).
Example results
Applications to fast NeRFs
Application to NeRF with sample reduction (DONeRF)
Application to NeRF with alternative representation (TensoRF)
Citation
@inproceedings{kaneko2023mimo-nerf,
title={{MIMO-NeRF}: Fast Neural Rendering with Multi-input Multi-output Neural Radiance Fields},
author={Takuhiro Kaneko},
booktitle={ICCV},
year={2023},
}