Tunneling-Based Self-Reconfiguration of Heterogeneous Sliding Cube-Shaped Modular Robots in Environments with Obstacles

Hiroshi Kawano

The results of this topic have been published in journal RAS, DARS2018, ICRA2018, ICRA2017 and IROS2015.

Papers are available from ICRA2017 IROS2015 DARS2018, RAS

Abstract: This paper studies a reconfiguration algorithm for heterogeneous cubic modular robots in environments with obstacles. Tunneling is suitable for the transformation of cubic modular robots in such an environment because a tunneling robot only passes spaces that are occupied by the robot in the start and goal configurations. We propose a method that realizes a tunneling reconfiguration for arbitrary arrangement of the start and goal configuration in which there are multiple and disconnected overlapped parts (In the previous method, the application is limited to the case with single connected overlapping part between the start and goal configuration.). The tunneling algorithm is implemented in distributed form. We have also designed a permutation algorithm that can be executed in the space used by the tunneling robot. Considering the application in environments with obstacles, for an instance of the tunneling modular robots, we assumed a usage of a motion primitive with only sliding motion along another module’s surface, which does not allows convex motions. We also assumes a usage of the three-dimensional 222 meta-module to guarantee the existence of mobile modules and maintain the connectivity of the robot structure during the tunneling and permutation processes. We show that the algorithm is complete for a connected robot structure with more than one meta-module and that the reconfiguration in an environment with obstacles is executed in quadratic operating time cost.

Tunneling method for the Multiple Overlapping Parts Case: (See DARS2018, RAS papers)

(1) 2x2x2 cubic meta-module structure with sliding only motion is assumed. The algorithm composed of homogeneous tunneling transformation and heterogeneous permutation processes.

(2) Tunneling is a transformation using snake like motion.

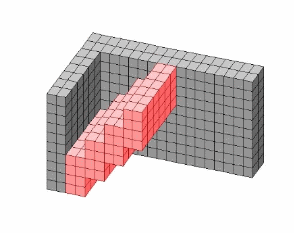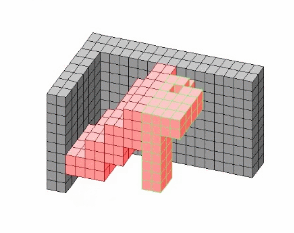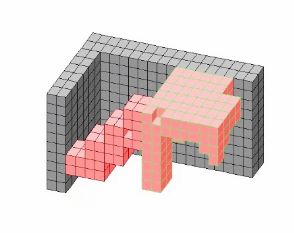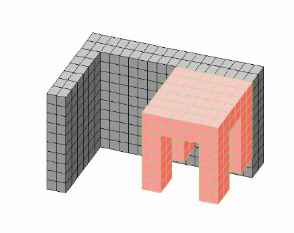
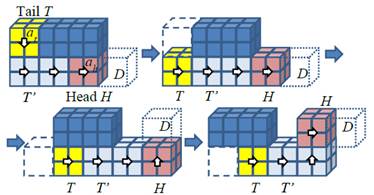
(3) A new method for selecting a head meta-module H that goes to the adjacent unfilled space in goal configuration (D) and the tail meta-module T is based on the method by Vassilvitskii [1], but additionally uses a set U_p of the positions that are once used as D and H. U_p acts like a single overlapped part between the current configuration and G. U_p is initialized to contain all positions of one of the S G parts at the beginning of the reconfiguration process. Every time each tunneling step motion is carried out, D is added to U_p. When U_p becomes adjacent to the position in one of the S G parts that are not included in U_p, all filled positions connected to U_p via G are added to U_p. H is selected only from U_p, and T is never selected from U_p.

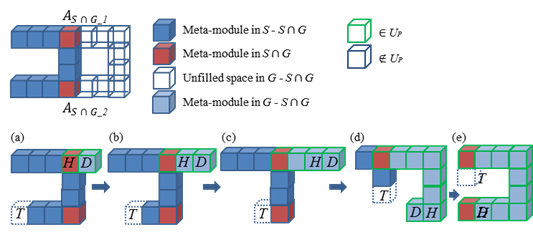
Tunneling meta-module control for Limited Sliding Cubic module: (See DARS2018, ICRA2017 papers)

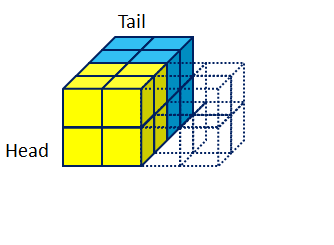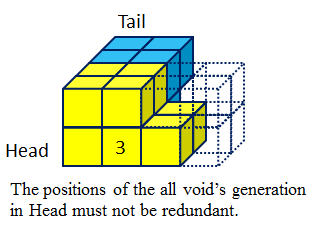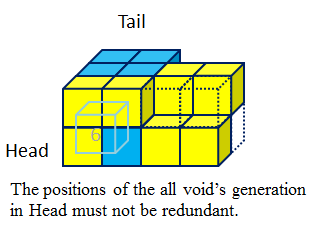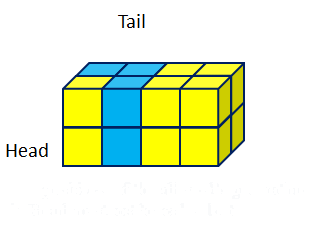
(4) We introduce Void Control method to implement a tunneling step motion using sliding cubes. A void is generated in the tunneling head H when one of the modules in H goes to the destinastion D. The generated void is navigated to T and ejected from T. Eight voids generation order in H is defined so as to keep the connectivity in H, D, and T. The proposed void generation order is available even in the case where H and T are adjacent, and this realizes the completeness of the tunneling for arbitrary size of the robot structure.

(5) An example of the tunneling reconfiguration between overlapped S and G with multiple overlapped parts.

Permutation method for Limited Sliding Cubic module: (See ICRA2017 papers)

(6) The permutation is carried out in the goal configuration after the tunneling transformation from the stat to the goal configuration. Only four modules are ejected from G to S in order to make the void spaces for position exchanging inside G. It is guaranteed that S - S G has at least one meta-modules position because S G. Therefore, the permutation process only need spaces provided by S G.

(7) The permutation is the repetition of the two modules position exchange using two void space in the goal configuration.

・Position exchange of two modules using two voids in a line and a corner.

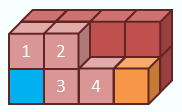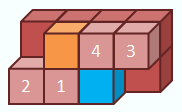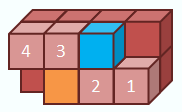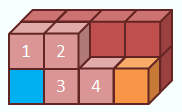
・Two modules in arbitrary relative positions are exchanged by combining the position exchanges in the line and the corner.

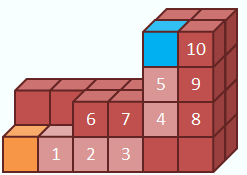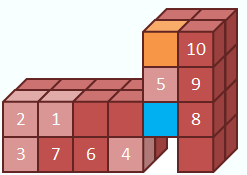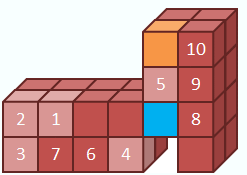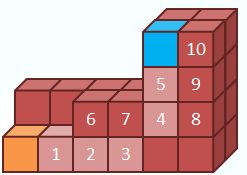
Tunneling method that prevents meta-module disassembling: (See RAS paper)

(8) We have also proposed a tunneling method that prevent each meta-module from disassembling through the tunneling process.

The tunneling motion in which the same meta-module with a camera keeps going ahead as the head meta-module repeatedly is available by the method.

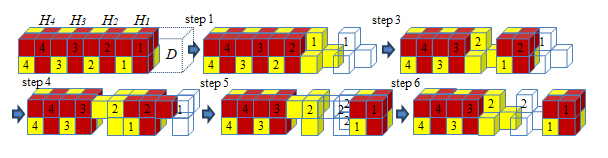
Reference

[1] S. Vassilvitskii, M. Yim, J. Suh, “A Complete, Local and Parallel Reconfiguration Algorithm for Cube Style Modular Robots,” in Proc.2002 IEEE Int. Conf. Robotics and Automation, pp. 117-122, Washington DC, May, 2002.

Last Updated on 2020.01.07