Linear Heterogeneous Reconfiguration of Cubic Modular Robots

via Simultaneous Tunneling and Permutation

Hiroshi Kawano

The results of this topic have been published in IEEE T-RO(PDF) and ICRA2019 (PDF).

Abstract: Reconfiguring heterogeneous modular robots in which all modules are not identical is much more time consuming than reconfiguring homogeneous ones, because ordinary heterogeneous reconfiguration is a combination of homogeneous transformation and heterogeneous permutation. While linear homogeneous transformation has been accomplished in previous research, linear heterogeneous permutation has not. The permutation process is in fact, the simple repetition of position exchange of modules in fully filled solid goal configuration or additional intermediate configuration. and is much time consuming. This research studies a reconfiguration algorithm for heterogeneous lattice modular robots with linear operation time cost. The algorithm is based on simultaneous tunneling and permutation, where a robot transforms its configuration via tunneling motion while permutation of each module’s position is performed simultaneously during the tunneling transformation. To achieve this, we introduce the idea of a transparent meta-module that allows modules belonging to a meta-module to pass through the spaces occupied by other meta-modules. We provide the proposed algorithm in both centralized and distributed form. We also prove the correctness and completeness of the proposed algorithm for a 222 cubic meta-module-based connected robot structure. We also show examples of the reconfiguration simulations of heterogeneous modular robots by the proposed algorithm.

(1) Homogeneous or Heterogeneous?

Homogeneous Reconfiguration:

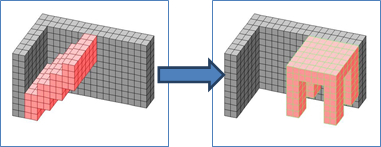
All modules are supposed to be identical. Therefore, the strict target position of each module is not defined in the goal configuration.

The reconfiguration algorithm only controls whole shape of the robot configuration.

Separate Permutation after

Homogeneous Transformation

is required.

Heterogeneous Reconfiguration:

All modules are supposed NOT to be identical. Therefore, each module has the strict target position in the goal configuration.

The reconfiguration algorithm navigates all modules to go to their specified target position in the goal configuration.

(2) Research Objective

While linear homogeneous reconfiguration has been accomplished in previous research, linear heterogeneous reconfiguration has not. This is because ordinary heterogeneous reconfiguration is a combination of homogeneous transformation and heterogeneous permutation. The permutation process is in fact, the simple repetition of position exchange of modules in fully filled solid goal configuration or additional intermediate configuration and is much time consuming. So we propose a method that solves the problem concerning the time consuming separate permutation. The proposed algorithm is based on simultaneous tunneling and permutation, where a robot transforms its configuration via tunneling motion while permutation of each module’s position is performed simultaneously during the tunneling transformation.

(3) Tunneling based transformation.

In tunneling based transformation, the robot changes its configuration by snake like motion. All modules in the tunneling snake follow the motion of the module at the tunneling head. Such a transformation approach has an advantage in saving space during the reconfiguration process. We can intuitively understand that the reconfiguration needs only the space provided by the start and goal configurations.

(4)Simultaneous Tunneling and Permutation

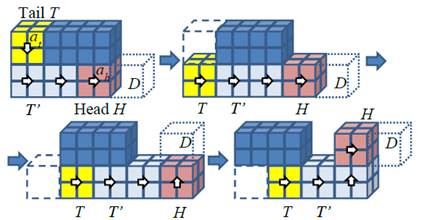
We introduce the idea of the transparent meta-module (hereafter TMM) to realize simultaneous tunneling and permutation to solve the problem. A TMM is defined to have void spaces inside it that allow the modules from other TMMs to pass through it (we call this property “transparency”). Let’s consider the case where a tunneling snake composed of TMMs contains a module whose target position is D. Because all TMMs are “transparent”, each module in the TMM snake can pass through other TMMs. Therefore, if the target position of the tail T is D, T can navigate to its target position D via void spaces in the TMMs in the snake. Even in cases where the target position of the TMM at the middle of the snake (M in the Figure) is D, we can navigate M to D by first letting the tail T go inside of M, then carrying out the position exchange between T and M, and finally letting M go to D. In these processes, tunneling and permutation are carried out simultaneously, and spaces outside the snake are not used. The time cost for one step motion of the tunneling (the motion where the tail T goes to D.) is linear whether the position exchange is carried out or not. If such tunneling processes are carried out in a constant time interval independent from the number of modules, the whole reconfiguration process takes linear operating time cost.

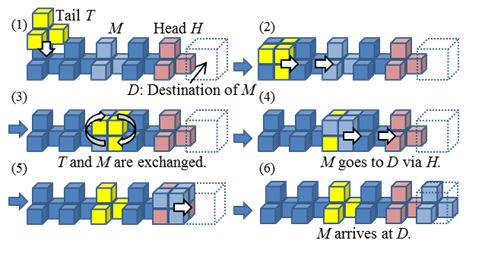
(5) Position Exchange of Transparent Cubic Meta-Modules.

Position exchange between two Transparent Cubic Meta Modules (TCMMs) is carried out in two adjacent 2 2 2 cubic spaces. Suppose the red TCMM and the yellow TCMM shown in the figures are to be exchanged. Fig. 1 shows the case where the direction from the red TCMM to the yellow TCMM is positive in the X, Y, or Z coordinate when position exchange starts [Fig. 1 (0)] (hereafter CASE+), and Fig. 2 shows the case where the direction from the red TCMM to the yellow TCMM is negative in the X, Y, or Z coordinate when position exchange starts [Fig. 2 (0)] (hereafter CASE-). In CASE+, no disconnection occurs for any arrangement of the LTCMMs adjacent to the yellow LTCMM; however, in CASE-, disconnection occurs when the yellow LTCMM has an adjacent LTCMM in the negative direction of the X, Y or Z axis. Therefore, before the red TCMM arrives at the neighbor position of the yellow TCMM, the arrangement of the TCMMs adjacent to the yellow TCMM must be checked before the start of the position exchange process. Whether CASE+ or CASE- is used is decided based on the result of the checking. Considering this, we propose a position exchange algorithm for TCMMs as follows:

Exchange(T₁, T₂):

1: Suppose T₁ is a movable LTCMM in R, or T₁ is a moving UTCMM in R and T₁ forms a CMM with a LTCMM in R.

2: If T₂ has at least one adjacent LTCMM T_next in the negative direction of the X, Y, or Z axis from T₂ in R, and T_next T₁, then

Move T₁ to the position of T_next via optimal path in R.

Carry out position exchange of T₁ and T₂ by CASE+.

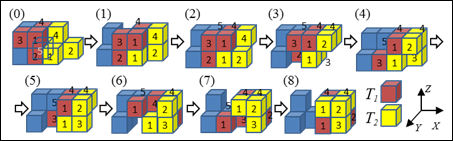Figure 1. (T₁ is red, and T₂ is yellow.)

3: Else, Suppose T_next T₁, and T_next is adjacent to T₂.

Move T₁ to the position of T_next via optimal path in R.

Carry out position exchange of T₁ and T₂ by CASE-.

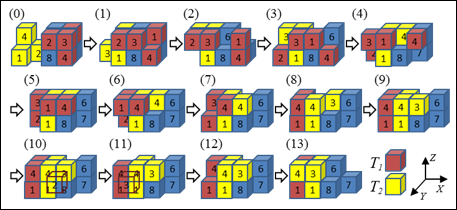Figure 2 (T₁ is red, and T₂ is yellow.)

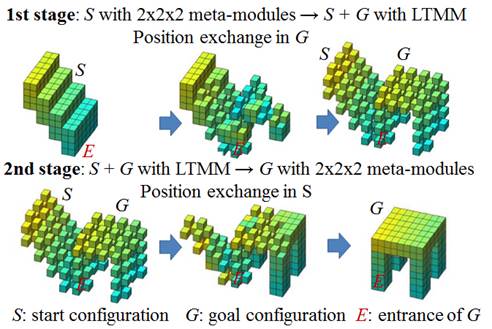
(6) Whole structure of the algorithm

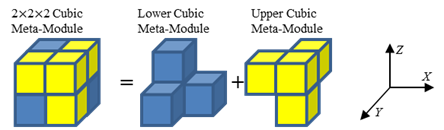
Let’s consider the reconfiguration of the 2x2x2Cubic Meta Module (CMM) based robot structure via simultaneous tunneling and permutation. A fully filled CMM-based structure has no spaces inside it through which TCMMs pass. Therefore, the reconfiguration algorithm must provide the spaces for their position exchange. We proposed the method that provides the space for TMM based position exchange using the space of both the start and goal configurations. The main strategy of the reconfiguration consists of two stages as follows:

First stage: The robot structure in the start configuration S is decomposed into S + G (G is the goal configuration) composed of Lower Cubic Meta-Modules (LCMM). Each Upper Cubic Meta-Module (UCMM) in S goes to its target position in G via one entrance position of G (hereafter, E). The UCMM in fully filled 2x2x2 CMM in S with the current smallest Manhattan distance from E priorly starts its navigation. Position exchange is executed in G.

Second stage: S + G are merged to G with 2x2x2 CMMs. Each LCMM in S goes to its target position via E. The LCMM in S with its target position that has the largest Manhattan distance from E priorly starts its navigation. Position exchange is executed in S.

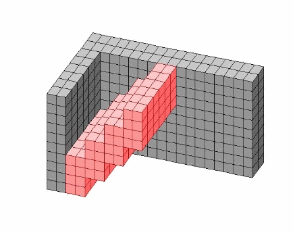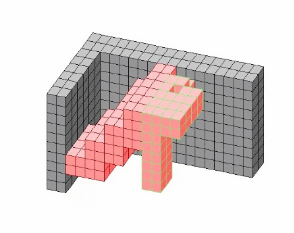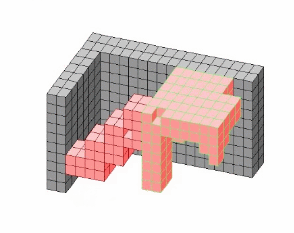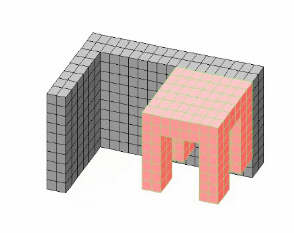
(7) Reconfiguration Example

Last Updated on 2019.12.20