Big Data Science
Extracting common patterns from multiple data sets
- Non-negative multiple matrix factorization: NM2F -
Abstract
We propose a novel matrix factorization method for heterogeneous data called Non-negative Multiple Matrix Factorization (NM2F), which utilizes parts of the data as auxiliary matrices that share the row or column indices of the target matrix. The performances of the factorization are improved by decomposing the target and auxiliary matrices simultaneously, since the auxiliary matrices provide additional information about the bases and coefficients. We examined NM2F in the real data experiments. The effect of the auxiliary matrices was confirmed by the improved NM2F performance. It was also confirmed that the bases obtained from the real data that NM2F exhibited intuitive and consistent patterns thanks to the non-negative constraint.
Photos
Poster
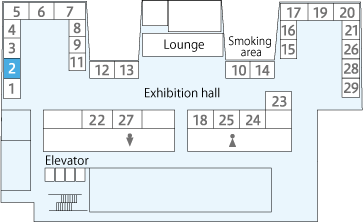
Map
Presentor

Masakazu Ishihata
Innovative Communication Laboratory
Innovative Communication Laboratory

Mathieu Blondel
Innovative Communication Laboratory
Innovative Communication Laboratory