

Learning of Automata using Recurrent Neural Networks
Abstract:
In learning of finite state automata(FSA)
by recurrent neural networks(RNN),
we propose a learning method
that stably trains RNN to simulate FSA from examples.
Given examples generated by an FSA,
it is difficult to identify the FSA.
For this problem, it is one approach
to infer an FSA by training an RNN to mimic examples.
When an RNN successfully learns an FSA,
orbits make clusters in a hidden space.
Since these clusters correspond
to states of the FSA, transitions among clusters make
the RNN behave like the FSA.
But, even if an RNN successfully learns to simulate an FSA,
orbits mostly get outside of clusters
for input data with a long length,
because of unstable transitions.
Consequently,
transitions are incorrect and
the RNN can not keep mimicking the FSA.
We found a theorem on the stability
of transitions among clusters[1]
and
proposed a new learning method based on the theorem[2].
Any FSA can be simulated by some RNN with binary threshold neurons.
A threshold function is equivalent to a sigmoid function with
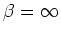 .
We usually employ a sigmoid function with finite
.
We usually employ a sigmoid function with finite 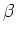 for learning.
In this case, it is not guaranteed that an RNN has the same
computational abilities as an FSA.
We have showed that
if
for learning.
In this case, it is not guaranteed that an RNN has the same
computational abilities as an FSA.
We have showed that
if 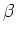 is greater than the critical value,
then, for data with an arbitrary length,
an RNN can maintain transitions among clusters
that are acquired by learning from examples.
Therefore,
the RNN can correctly simulate the learned FSA
for unknown test data.
This means that
an RNN with finite
is greater than the critical value,
then, for data with an arbitrary length,
an RNN can maintain transitions among clusters
that are acquired by learning from examples.
Therefore,
the RNN can correctly simulate the learned FSA
for unknown test data.
This means that
an RNN with finite 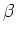 can perfectly mimic an FSA.
Moreover, when
can perfectly mimic an FSA.
Moreover, when 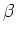 is sufficiently large,
behaviors of any RNN are equivalent to that of FSA.
is sufficiently large,
behaviors of any RNN are equivalent to that of FSA.
If 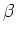 is sufficiently large,
then it is expected that orbits stably move
from cluster to cluster for data with an arbitrary length.
But, in this case,
it is hard for an RNN to learn to mimic an FSA
since an error surface forms a steep stair-like landscape.
We propose a learning method that gradually increases
is sufficiently large,
then it is expected that orbits stably move
from cluster to cluster for data with an arbitrary length.
But, in this case,
it is hard for an RNN to learn to mimic an FSA
since an error surface forms a steep stair-like landscape.
We propose a learning method that gradually increases 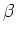 .
But, after a long term learning,
.
But, after a long term learning,
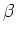 becomes large and the error surface has narrow steep valleys,
then it is hard to learn effectively.
To prevent jumping out of valleys,
we adaptively control the value
of modification gap of
becomes large and the error surface has narrow steep valleys,
then it is hard to learn effectively.
To prevent jumping out of valleys,
we adaptively control the value
of modification gap of 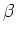 and learning rate.
The experiments showed
an RNN learns to get stable cluster transitions
faster and stably(Figure 1).
and learning rate.
The experiments showed
an RNN learns to get stable cluster transitions
faster and stably(Figure 1).
Contact: Kenichi Arai, Email:ken@cslab.kecl.ntt.co.jp
Figure 1:
Comparison of learning
(Comparison of stability(Left) and convergence time(Right))
|
- 1
-
Arai, K. and Nakano, R.:
Annealed RNN learning of finite state automata,
Proc. of the 6th International Conference
on Artificial Neural Networks (ICANN'96),
pp. 519-524 (1996).
- 2
-
Arai, K. and Nakano, R.:
Adaptive
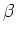 scheduling method of finite state automata
by recurrent neural networks,
Proc. of the 4th International Conference
on Neural Information Processing(ICONIP'97),
pp. 351-354 (1997).
scheduling method of finite state automata
by recurrent neural networks,
Proc. of the 4th International Conference
on Neural Information Processing(ICONIP'97),
pp. 351-354 (1997).


This page is assembled by Takeshi Yamada
![\includegraphics[height=4.8cm]{arai-1.ps}](araiimg3.gif)
![\includegraphics[height=4.8cm]{arai-2.ps}](araiimg4.gif)