Up

Logic Optimization by Effective Decompositions

Abstract

We have developed a method for a simple disjunctive decomposition, which definitely improves the quality of a logic circuit. The method finds decomposition forms by detecting symmetric variables and constructs new logic circuits by utilizing the original circuit structure.

Background

Decomposing a function f into smaller functions is a frequent operation in logic circuit optimization. Simple disjunctive decomposition f(X, Y) = h(g(X), Y) is a special case where two new functions have no common variables and g is a single-output function. It offers an optimal circuit structure for a single-output function. Although it does not exist in all functions, if it exists in a function, we can improve circuit quality by detecting and applying it.

Finding Decomposition Forms

To find decomposition forms efficiently, we limit the types of decomposition forms to be found to two as shown in Figure 1. Even if we limit the forms in such a way, we expect that the other decomposition forms can be found by recursively applying these two. Actually, we have found almost all simple disjunctive decompositions existing in given functions using this method [1].

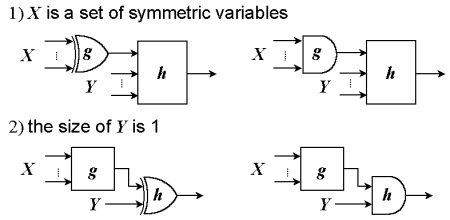
Fig. 1: Decomposition forms
Fig. 1: Decomposition forms

Constructing New Circuits After Decomposition

Since operations for the decomposition are performed on the function represented by a circuit, we do not have the new circuits G and H that represent the new functions g and h. It is possible for us to construct them through an ordinary logic synthesis process from new functions. However, the process takes a lot of time and may ignore the good structure of the original circuit F. We have discovered that G and H can be obtained by simply assigning constant values to variables in the original circuit F [2]. In Figure 2, G is obtained by assigning 0 to c of F. Similarly, H is obtained by assigning 1 to b of F and replacing a with g'.

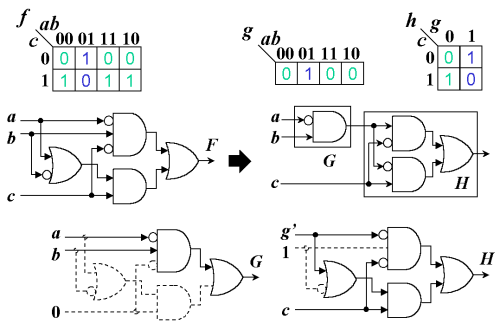
Fig. 2: Constructing new circuits
Fig. 2: Constructing new circuits

Experimental Results

In experiments using benchmark circuits, we achieved an overall improvement of 9% in the circuit area with an execution overhead time of several seconds.

Future Work

We will clarify the applicable domain and integrate these methods into PARTHENON system.

References

[1]
Sawada, H., Yamashita, S. and Nagoya, A.: Restricted Simple Disjunctive Decompositions Based on Grouping Symmetric Variables, Proc. of the 7th Great Lakes Symposium on VLSI, pp. 39-44 (1997).
[2]
Sawada, H., Yamashita, S. and Nagoya, A.: Restructuring Logic Representations with Easily Detectable Simple Disjunctive Decompositions, Proc. of Design, Automation and Test in Europe Conference 1998 (DATE '98), pp. 755-759 (1998).
Contact: Hiroshi Sawada; Email: sawada@cslab.kecl.ntt.co.jp
Last modified: Wed Oct 14 15:54:55 1998