Law Discovery using Neural Networks

Abstract:

To discover an underlying law from a set of numeric data obtained in the scientific or industrial fields, we have developed a new algorithm called RF5 [1,2,3].

RF5 Algorithm

It is possible to discover monomial laws or polynomial laws whose power values are integers, by adopting least squares methods or combinatorial search methods. However, these methods are hardly applicable for discovering complex polynomial laws whose power values are not restricted to integers.

The law discovery problem can be formalized as learning in neural networks. However, training this type of neural networks is quite tough, and the standard BP algorithm works quite poorly for this type or training. Thus, in order to efficiently and constantly obtain good results, we have developed a new second-order learning algorithm called BPQ [4]: by adopting a quasi-Newton method as a basic framework, the descent direction is calculated on the basis of a partial BFGS update and a reasonably accurate step-length is efficiently calculated as the minimal point of a second-order approximation. In general, for a given set of data, we cannot know the optimal number of hidden units in advance, and the law-candidate which minimizes training error is not always the best one. In RF5, the MDL criterion is adopted to adequately evaluate the law-candidates.

Experiments showed that RF5 successfully discovered underlying laws whose power values are not restricted to integers, even if the data contained a small amount of noise and irrelevant variables (Table 1).

Future Work

We are examining applicability to dynamical system identification, economical demand prediction, and so on. Incidentally, if only a set of data is provided, by discovering law-candidates in Communication Science Laboratories, we can show them.

 

Table 1: Examples of discovered laws

law name	original law	discovered law	# samples
Hagen-Rubens' law	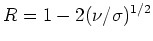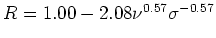$R = 1-2({\nu}/{\sigma})^{1/2}$	$R = 1.00-2.08\nu^{0.57}\sigma^{-0.57}$	9
Kepler's third law	T = 0.41r3/2	T = 0.19+0.41r1.50	5
Boyle's law	V = 29.30/p	V = -0.61+29.05p-1.08	19
artificial law 1*	y = 2+3x1x2+4x3x4x5	y = 2.0+3.0x11.0x21.0+4.0x31.0x41.0x51.0	200
artificial law 2*	y = 2+3x1-1x23+4x3x41/2x5-1/3	y = 2.0+3.0x1-1.0x23.0+4.0x31.0x40.5x5-0.3	200
(*) these data include irrelevant variables ( $x_6 \sim x_9$).

 

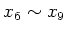Contact: Kazumi Saito, Email: saito@cslab.kecl.ntt.co.jp

Bibliography

1

Saito, K. and Nakano, R.:
Law Discovery using Neural Networks,
Proc. of NIPS*96 Post-conference Workshop (Rule-extraction from Trained Neural Networks), pp. 62-69 (1996).

2

Saito K. and Nakano, R.:
A Connectionist Approach to Numeric Law Discovery,
Machine Intelligence 15 (to appear).

3

Saito, K. and Nakano, R.:
Law Discovery using Neural Networks,
Proc. of the 15th International Joint Conference on Artificial Intelligence (IJCAI '97), pp. 1078-1083 (1997).

4

Saito, K. and Nakano, R.:
Partial BFGS Update and Calculating Optimal Step-length for Three-layer Neural Networks,
Neural Computation, Vol. 9, No. 1, pp. 123-141 (1997).

Last modified on: Sat Jan 23 19:57:56 1999