Learning Ensemble Classifiers

Abstract:

Focusing on classification problems, we have developed a new method for linearly combining multiple neural network classifiers based on the statistical pattern recognition theory. Experimental results show that the proposed method can construct a better combined classifier which outperforms the best single classifier in terms of the overall classification errors for test data.

Background

It has been shown that combining multiple unstable estimators such as neural networks (NNs) results in decreasing classification errors for test data, and as a result, the combining of estimatiors is regarded as a variance reducing device [1][2]. Ideally, however, such combination of estimators should take advantage of the strengths of the individual estimators, avoid their weaknesses, and improve all of the individual estimators.

For classification problems, since the complexity of class boundaries is not necessarily uniform over all classes in a feature space, it is possible to develop a situation where a classifier works best for a class, while another classifier works best for another class. In such a case, we expect the combination of these classifiers to improve on both. Our method is motivated by an attempt to achieve such an ideal combination for improving the classification performance.

Optimal Weighting

In this approach, by changing a regularization paramter, several NNs are first selected, each of which works best for each class. Then, they are combined with the optimal linear weights. Although a few optimal weighting methods exist, they are not suitable for classification tasks because they are formulated in the regression context using the minimum squared error (MSE) criterion. In our method, the problem of estimating linear weights in combination is reformulated as the problem of designing linear discriminant functions using the minimum classification error (MCE) criterion [3]. In this formulation, because the classification decision rule is incorporated into the cost funtion, better combination weights suitable for the classificaition objective can be obtained.

Experimental Results

Table 1 (2) shows the average classification errors of a single (combined) classifier over ten runs for a four class problem. We can see that the proposed method (MCE) provided the best result (22.2%), which was very close to the true error (Bayes error: 22.1%). Moreover, we can see that our combination scheme could certainly improve the best single classifier (23.3%).

 

Table 1: Average classification errors and (standard deviations) % for single NN

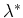$\lambda^*$	0.7	0.0282	0.343	0.0576
Training	28.7	19.5	24.3	19.2
data	(1.53)	(0.68)	(0.63)	(0.34)
Test	27.0	25.0	24.1	23.3
data	(0.55)	(0.27)	(0.24)	(0.29)

 

 

Table 2: Average classification errors and (standard deviations) % by combination

	Majority	Simple	Linear Comb.
	voting	averaging	MSE	MCE
Training	19.4	19.2	20.0	20.4
data	(0.36)	(0.27)	(0.42)	(0.36)
Test	23.4	23.4	23.0	22.2
data	(0.26)	(0.21)	(0.35)	(0.33)

 

Contact: Naonori Ueda, Email: ueda@cslab.kecl.ntt.co.jp

Bibliography

1

Ueda, N. and Nakano, R.: Generalization error of ensemble estiamtors, Proc. of International Conference on Neural Networks (ICNN'96), pp. 90-95 (1996).

2

Ueda, N. and Nakano, R.: Analysis of generalization error on ensemble learning (in Japanese), IEICE Trans. D-II, Vol. J80_DII, No. 9, pp. 2512-2521 (1997).

3

Ueda, N. and Nakano, R.: Combining discriminant-based classifiers using the minimum classification error discriminant, Proc. of Neural Networks for Signal Processing (NNSP'97), pp. 365-374 (1997).