

Deterministic Annealing EM Algorithm
Abstract:
The EM algorithm is an iterative statistical technique for computing
maximum likelihood parameter estimates from incomplete data. It has
been employed to a wide variety of parameter estimation problems.
However, this algorithm has the local maxima problem in
practice (Figure
1(a)). Although the problem is familiar to many,
little effort has been made so far.
Figure 1:
Estimation results
m1, m2denote unknown paramters. In DAEM algorithm, search results at
each temerature are superimposed on the free energy at 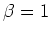 .
![\includegraphics[width=12.5cm]{ueda-1.epsi}](ueda-DAEMimg2.gif) |
To overcome this problem, we have derived the deterministic
annealing EM (DAEM) algorithm by using the principle of
maximum entropy and the statistical mechanics
analogy [1]
[3].
In this approach, the maximization of the likelihood function is
embedded in the minimization of the thermodynamic free energy
depending on the temperature which controls the annealing process.
As shown in Figure 2,
by gradually decreasing the temperature (increasing 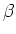 )
until
)
until
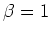 (when
(when 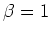 ,
F exactly agrees
with the likelihood function) and minimizing the free energy at each
temperature, the global optimal solution can be obtained.
Note that unlike the conventional simulated annealing (SA), the free
energy is deterministically minimized at each temperature.
Therefore the DA is much faster than the SA.
,
F exactly agrees
with the likelihood function) and minimizing the free energy at each
temperature, the global optimal solution can be obtained.
Note that unlike the conventional simulated annealing (SA), the free
energy is deterministically minimized at each temperature.
Therefore the DA is much faster than the SA.
Figure 2:
Annealing control by the temperature
The optimization
at each temperature starts from
the optimal point obtained at the previous temperature. As the
value of 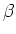
approaches one, the solution is gradually led to
the true solution.
![\includegraphics[width=15.6cm]{ueda-2.epsi}](ueda-DAEMimg4.gif) |
We have applied the DAEM algorithm to the training of a probabilitic
neural network using mixture models and have shown its
superiority [2]
[3].
Contact: Naonori Ueda, Email: ueda@cslab.kecl.ntt.co.jp
- 1
-
Ueda, N. and Nakano, R.: Deterministic annealing variant of the EM
algorithm, G. Tesauro et al. eds.,
Advances in NIPS 7, MIT Press, Cambridge MA, pp.545-552 (1995).
- 2
-
Ueda, N. and Nakano, R.: A new maximum likelihood training and application to
probabilistic neural networks, Proc. of Int. Conf. on Artificial
Neural Networks (ICANN)'95, pp. 497-501 (1995).
- 3
-
Ueda, N. and Nakano, R.: Deterministic annealing EM algorithm,
Neural Networks , vol. 11, no. 2, pp. 271-282 (1998).


This page is assembled by Takeshi Yamada
![\includegraphics[width=12.5cm]{ueda-1.epsi}](ueda-DAEMimg2.gif)
![\includegraphics[width=12.5cm]{ueda-1.epsi}](ueda-DAEMimg2.gif)
![]() )
until
)
until
![]() (when
(when ![]() ,
F exactly agrees
with the likelihood function) and minimizing the free energy at each
temperature, the global optimal solution can be obtained.
Note that unlike the conventional simulated annealing (SA), the free
energy is deterministically minimized at each temperature.
Therefore the DA is much faster than the SA.
,
F exactly agrees
with the likelihood function) and minimizing the free energy at each
temperature, the global optimal solution can be obtained.
Note that unlike the conventional simulated annealing (SA), the free
energy is deterministically minimized at each temperature.
Therefore the DA is much faster than the SA.
![\includegraphics[width=15.6cm]{ueda-2.epsi}](ueda-DAEMimg4.gif)