Relational data analysis by infinite trees

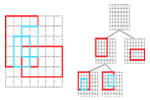
We are aiming at establishing a technical basis of infinite data analysis, which we believe is a generalized paradigm beyond big data analysis. While big data analysis has been one of the very active research topics in the machine learning field, the amount of data for the analysis has been considered finite, as implied by the term “big data” itself. However, many types of data would intrinsically grow infinitely in size, and the observed data should naturally be regarded as just a part of a potentially infinite amount of data. A key to the infinite data analysis, such as clustering and factorization, is a stochastic process, or an infinite-dimensional probabilistic model, such as Dirichlet process, Mondrian process, and rectangular tiling process [2]. Recently, we have proposed a novel stochastic process that has a capability of representing arbitrary R-trees within a matrix of infinite size. We show its principle and demonstrate its application to relational data analysis.

Please click the thumbnail image to open the full-size PDF file.