| 05 |
A mathematical link for light-matter interactionNew unification through non-commutative harmonic oscillators 
|
|---|
We have demonstrated that the purely mathematical model “non-commutative harmonic oscillator” is essentially equivalent to the physical model “two-photon quantum Rabi model”, which describes light-matter interaction. We have also revealed the relationship between these models and the “one-photon quantum Rabi model”, differing only in the number of photons. The proof relied on the principle of symmetry in fundamental mathematics. These results bridge mathematical and physical models, allowing us to apply accumulated research on mathematical models to the theoretical understanding of physical systems governing light-matter interaction. Through these discoveries, we aim to develop new technologies and theories applicable to the advancement of quantum computers by connecting quantum physics and mathematics. Furthermore, we seek to solve open problems and develop novel theories in fundamental mathematics (such as number theory) from the perspective of quantum physics.
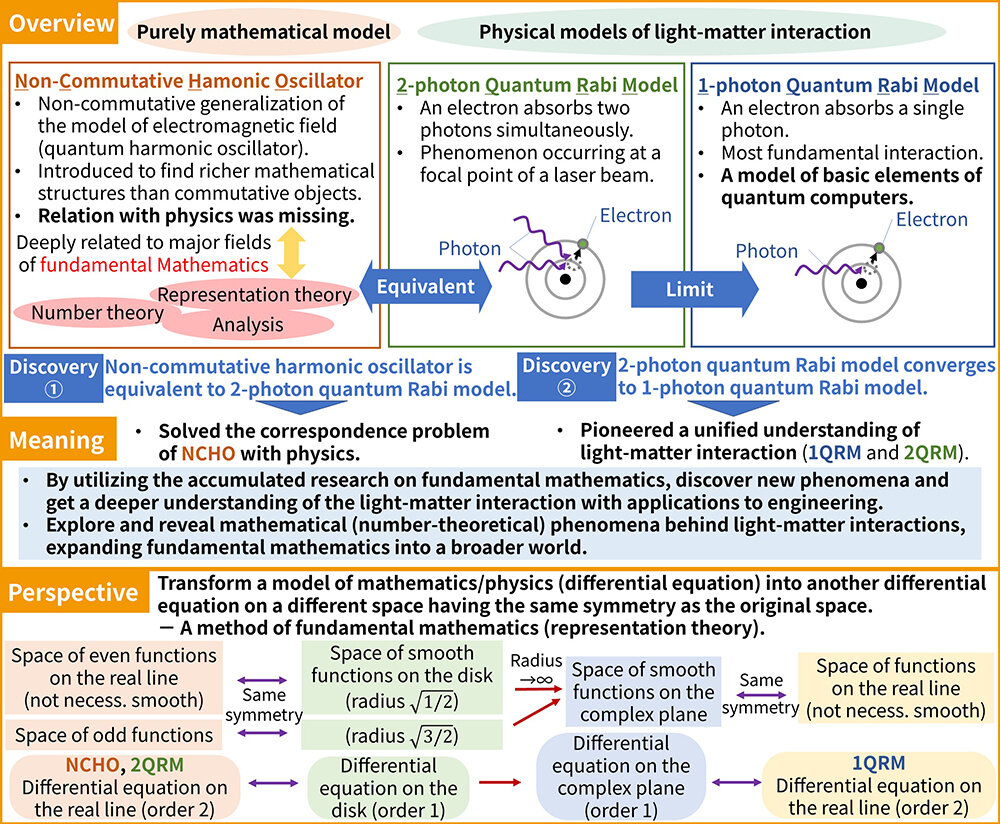
[1] K. Kimoto, C. Reyes-Bustos, M. Wakayama, “Determinant expressions of constraint polynomials and the spectrum of the asymmetric quantum Rabi model,” Int. Math. Res. Not. IMRN, No. 12, pp. 9458–9544, 2021.
[2] R. Nakahama, “Representation theory of sl(2,R)≃su(1,1) and a generalization of non-commutative harmonic oscillators,” Mathematical Foundations for Post-Quantum Cryptography, Springer, p. 20, 2025, in press, arXiv:2310.17118.
[3] R. Nakahama, “Equivalence between non-commutative harmonic oscillators and two-photon quantum Rabi models,” Int. Math. Res. Not. IMRN, No. 7, rnaf066, p. 9, 2025, arXiv:2405.19814.
[4] C. Reyes-Bustos, M. Wakayama, “Covering families of the asymmetric quantum Rabi model: η-shifted non-commutative harmonic oscillators,” Comm. Math. Phys. Vol. 403, No. 3, pp. 1429–1476, 2023.
Ryosuke Nakahama, Computing Theory Research Group, Media Information Laboratory / Institute for Fundamental Mathematics




