| 13 |
数の不思議はどこから生まれる?一般化モチーフ理論を用いた新たな数論的現象の解明 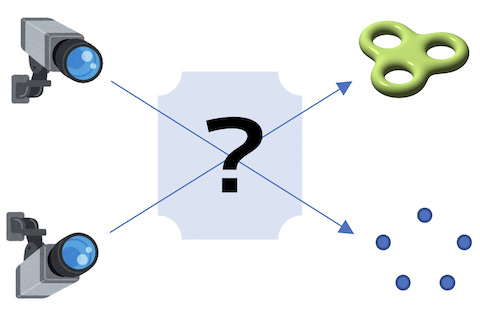
|
|---|
| どんな研究 |
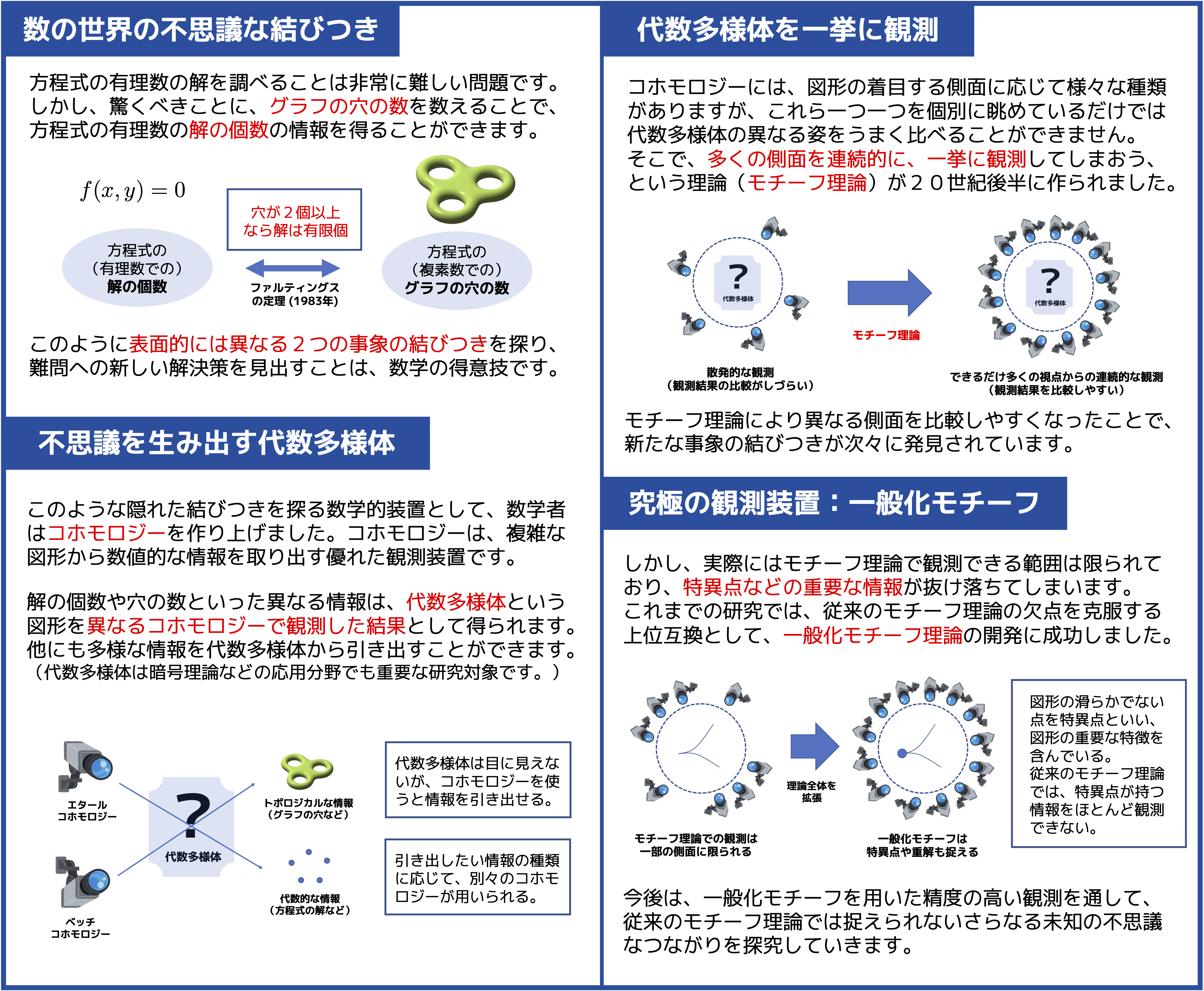
数学では、一見まったく異なる2つの事柄が結びつくことがよくありますが、それは単なる偶然ではないはずです。本研究では、発表者がこれまでに開発した一般化モチーフ理論を用いて、数の世界の不思議な結びつきが生み出される本質的なメカニズムを明らかにします。 |
|---|---|
| どこが凄い |
数の研究は、代数多様体という図形の研究に置き換えられます。一般化モチーフ理論は、代数多様体をあらゆる視点から一挙に観測する数学的装置です。別々の視点(=コホモロジー)から眺めた代数多様体の姿は一見、全く異なりますが、一般化モチーフ理論で隙間なく観測することで、異なる視点を結びつけることができます。 |
| めざす未来 |
代数多様体の究極の観測装置である一般化モチーフ理論を用いれば、表面的には全く異なる2つの事柄を、偶然に頼らず系統的に結びつけることができます。本研究を推進することにより、人類の活動をいたるところで支える数の真理の探究を爆発的に加速させることができると期待されます。 |
[1] B. Kahn, H. Miyazaki, S. Saito, T. Yamazaki, “Motives with modulus, III,” Annals of K-theory (to appear).
[2] B. Kahn, H. Miyazaki, S. Saito, T. Yamazaki, “Motives with modulus, II,” Epijournal de Geometrie Algebrique, Vol. 5, epiga:7115, 2021.
[3] B. Kahn, H. Miyazaki, S. Saito, T. Yamazaki, “Motives with modulus, I,” Epijournal de Geometrie Algebrique, Vol. 5, epiga:7114, 2021.
[4] B. Kahn, H. Miyazaki, “Topologies on schemes and modulus pairs,” Nagoya Mathematical Journal, Vol. 244, pp. 283?313, 2021.
[5] H. Miyazaki, “Nisnevich topology with modulus,” Annals of K-theory, Vol. 5, pp. 581?604, 2019.
宮﨑 弘安(Hiroyasu Miyazaki) 基礎数学研究センタ
Email: cs-openhouse-ml@hco.ntt.co.jp



