研究展示
| 22 |
代数・幾何・解析をつなぎ新たな発見をめざす保型形式の級数展開と構造定理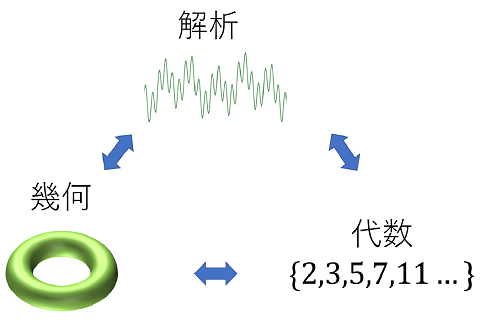 
|
|---|
| どんな研究 |
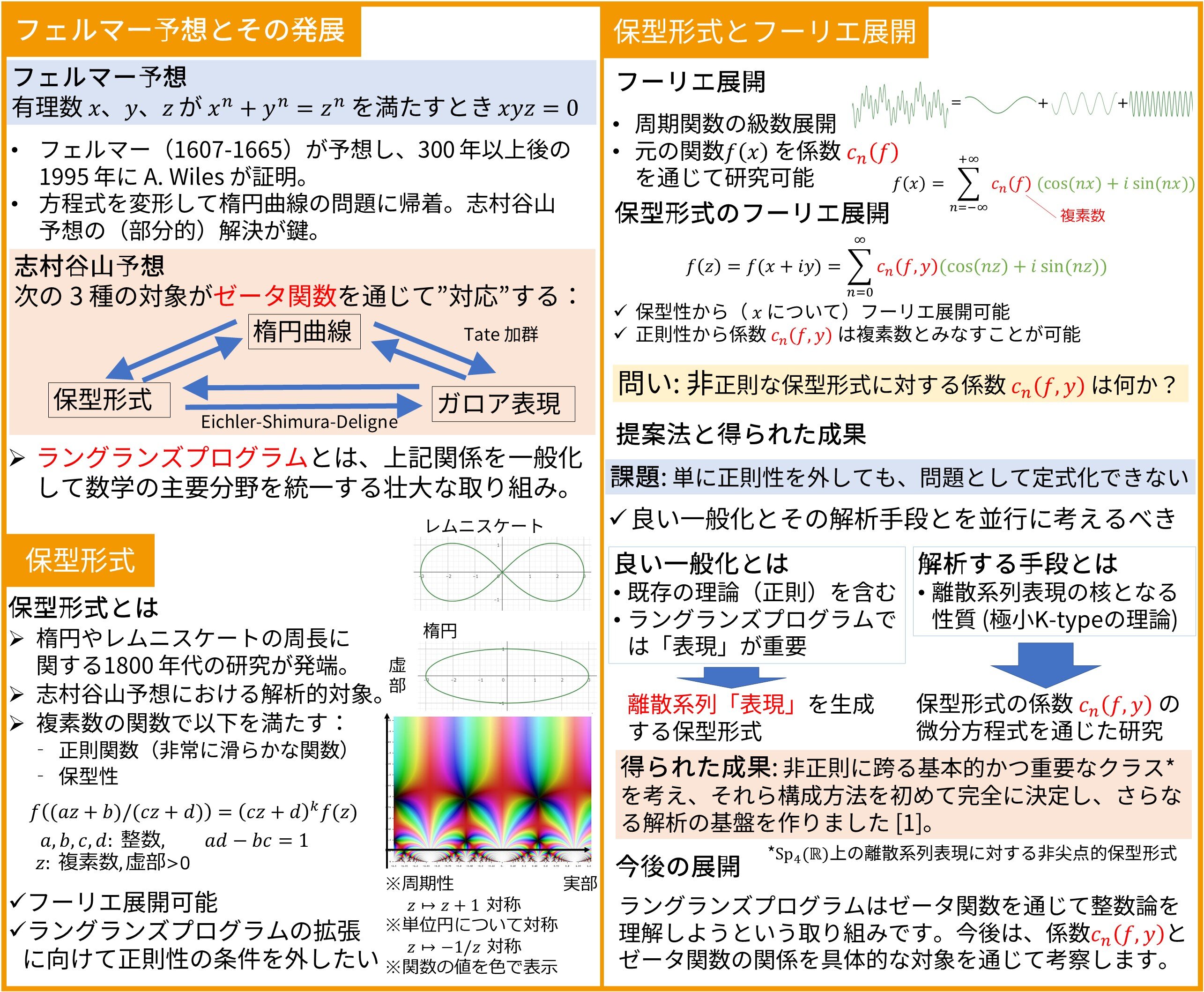
３００年以上にわたり未解決だったフェルマーの最終定理の証明では、代数・幾何・解析といった数学の領域をつなぐ「保型形式」の理論が決定的な役割を果たしました。この理論の拡張に向け、対象とするクラスの保型形式の構成方法とその級数展開を決定しました。 |
|---|---|
| どこが凄い |
保型形式は非常に滑らかな関数で、かつ強い対称性を持ちます。既存の保型形式の枠組みを超える数学的発見のためには、滑らかさの条件を緩めることが必要ですが、その分、解析が困難になります。解析が可能でありつつ条件を緩めたうえで、解析手法と構成方法を明らかにしました。 |
| めざす未来 |
保型形式の理論を通じ、ムーンシャイン予想など大きな予想が解決されてきました。その中には最密球充填問題等の自然現象に潜む数学に関するものも多くあります。本研究を基礎とし、更なる数学的発見を行い、ラングランズ予想など数学の大予想の解決にも貢献することをめざします。 |
[1] S. Horinaga, H. Narita, “Cuspidal components of Siegel modular forms for large discrete series representations of 
,”manuscripta mathematica
, pp. 1-44, 2023
堀永 周司 (Shuji Horinaga) メディア情報研究部 情報基礎理論研究グループ ／ 基礎数学研究センタ