研究展示
| 05 |
つながり関係からグループを見つける無限の柔軟度を持つ関係データモデル 
|
|---|
| どんな研究 |
ソーシャルネットワーキングサービスにおける利用者の繋がり関係や、商品群に対するユーザの購買履歴など、ネットワーク・グラフを含む関係データは、我々の身近に現れます。本研究では、関係データの中に隠れたグループを見つけることを目的としています。 |
|---|---|
| どこが凄い |
関係データからグループを見つける際、グループの数やサイズを人手で適切に設定するのは困難です。そこで、グループの数やサイズを入力データのサイズや性質に応じてデータ駆動的に自動調整してくれる能力を持った関係データ解析手法を提案しました。 |
| めざす未来 |
関係データの中に潜むグループを見つけ出すことによって、そのデータを特徴づける重要な性質を明らかにすることがあります。より大規模な関係データから適切なグループを見つけ出すことで、より効率的に情報を保管・探索・検索するため技術の発展へ貢献していきます。 |
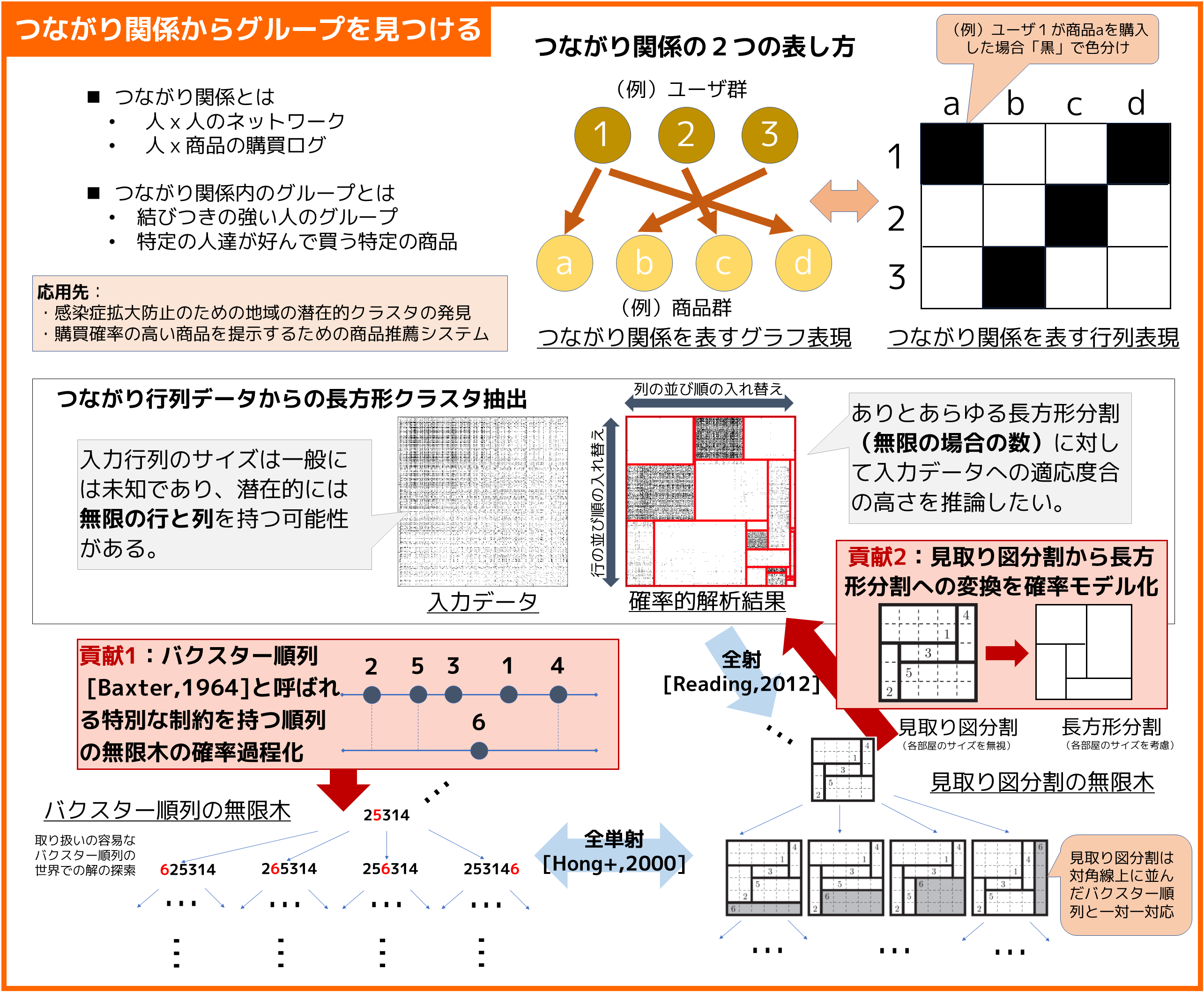
[1] M. Nakano, A. Kimura, T. Yamada, N. Ueda, “Baxter Permutation Process,” in Proc. Advances in Neural Information Processing Systems 33 (NeurIPS), 2020.
動画の公開は終了いたしました。ご了承くださいますようお願いいたします。
Q&A の公開は終了いたしました。ご了承くださいますようお願いいたします。
中野 允裕 (Masahiro Nakano) メディア情報研究部 メディア認識研究グループ
Email: cs-openhouse-ml@hco.ntt.co.jp


